Limits by Logarithms, Squeeze Theorem, and Euler’s Constant

by Justin Skycak (@justinskycak) on January 02, 2019

Various tricks for evaluating tricky limits.

This post is part of the book Justin Math: Calculus. Suggested citation: Skycak, J. (2019). Limits by Logarithms, Squeeze Theorem, and Euler's Constant. In Justin Math: Calculus. https://justinmath.com/limits-by-logarithms-squeeze-theorem-and-eulers-constant/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

A useful property of limits is that they can be brought inside continuous functions, i.e. the limit of a continuous function is the function of the limit.

For example, $\sqrt{x}$ is a continuous function, so to take the limit of the square root of some expression, we can first find the limit of the expression and then take the square root.

$\begin{align*} \lim\limits_{x \to \infty} \sqrt{\frac{2x}{x+1}} = \sqrt{\lim\limits_{x \to \infty} \frac{2x}{x+1}} = \sqrt{2} \end{align*}$

We can do the same thing with other continuous functions, such as $\ln x$.

$\begin{align*} &\lim\limits_{x \to 2^+} \left[ \ln (x^2-x-2) - \ln(x^2-3x+2) \right] \\ &= \lim\limits_{x \to 2^+} \ln \left( \frac{x^2-x-2}{x^2-3x+2} \right) \\ &= \ln \left( \lim\limits_{x \to 2^+} \frac{x^2-x-2}{x^2-3x+2} \right) \\ &= \ln \left( \lim\limits_{x \to 2^+} \frac{(x-2)(x+1)}{(x-2)(x-1)} \right) \\ &= \ln \left( \lim\limits_{x \to 2^+} \frac{x+1}{x-1} \right) \\ &= \ln 3 \end{align*}$

Exponential Limits

Logarithms in particular are useful for evaluating exponential limits, which have variables in both the limit and the base.

For example, to evaluate the limit

$\begin{align*} \lim\limits_{x\to 0^+} x^{\ln x} \end{align*}$

it is easiest to start by evaluating the logarithm of the limit.

$\begin{align*} &\ln \left( \lim\limits_{x\to 0^+} x^{\ln x} \right) \\ &= \lim\limits_{x\to 0^+} \ln \left( x^{\ln x} \right) \\ &= \lim\limits_{x\to 0^+} (\ln x) \ln x \\ &= \lim\limits_{x\to 0^+} (\ln x)^2 \\ &= \left( \lim\limits_{x\to 0^+} \ln x \right)^2 \\ &= (-\infty)^2 \\ &= \infty \end{align*}$

Since we know the logarithm of the limit is $\infty$, the limit is just $e$ raised to the power of $\infty$.

$\begin{align*} \lim\limits_{x\to 0^+} x^{\ln x} = e^{\infty} = \infty \end{align*}$

Using the same process, we can show that

$\begin{align*} \lim\limits_{x\to 0^+} x^{(\ln x)^2} = e^{-\infty} = 0 \end{align*}$

because this time, the logarithm of the limit evaluates to $-\infty$.

$\begin{align*} &\ln \left( \lim\limits_{x\to 0^+} x^{(\ln x)^2} \right) \\ &= \lim\limits_{x\to 0^+} \ln \left( x^{(\ln x)^2} \right) \\ &= \lim\limits_{x\to 0^+} (\ln x)^2 \ln x \\ &= \lim\limits_{x\to 0^+} (\ln x)^3 \\ &= \left( \lim\limits_{x\to 0^+} \ln x \right)^3 \\ &= (-\infty)^3 \\ &= -\infty \end{align*}$

Squeeze Theorem

Another useful trick for evaluating difficult limits is squeezing them between limits that are easier to evaluate.

For example, to evaluate the limit

$\begin{align*} \lim\limits_{x \to \infty} \frac{\sin x}{x} \end{align*}$

we can make use of the fact that $\sin x$ is bounded between $-1$ and $1$. Then as $x \to \infty$ we have the following:

$\begin{align*} -1 &\leq \hspace{.45cm} \sin x \hspace{.45cm} \leq 1 \\ \frac{-1}{x} &\leq \hspace{.425cm} \frac{\sin x}{x} \hspace{.425cm} \leq \frac{1}{x} \\ \lim\limits_{x \to \infty} \frac{-1}{x} &\leq \lim\limits_{x \to \infty} \frac{\sin x}{x} \leq \lim\limits_{x \to \infty} \frac{1}{x} \\ 0 &\leq \lim\limits_{x \to \infty} \frac{\sin x}{x} \leq 0 \end{align*}$

The inequality states that the limit must be between $0$ and $0$, and the only number that is between $0$ and $0$ is $0$ itself, so by the squeeze theorem, the limit must evaluate to $0$.

$\begin{align*} \lim\limits_{x \to \infty} \frac{\sin x}{x} =0 \end{align*}$

In other words, the limit must be $0$ because we squeezed it between two other limits, both of which evaluate to $0$.

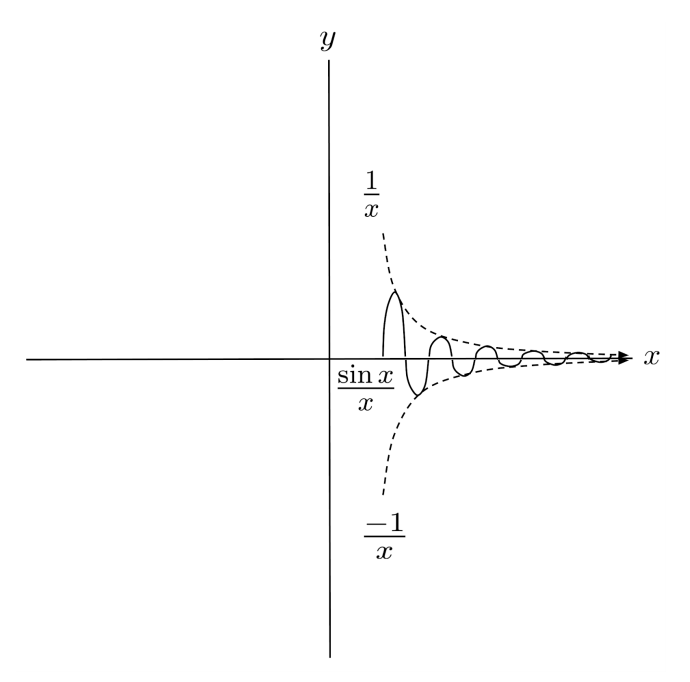
As another example, we can show that

$\begin{align*} \lim\limits_{x\to 0} x \cos \left( \frac{1}{x} \right) = 0 \end{align*}$

by performing a squeeze between the bounds of $\cos$:

$\begin{align*} \lim\limits_{x\to 0^-} x (-1) &\leq \lim\limits_{x\to 0} x \cos \left( \frac{1}{x} \right) \leq \lim\limits_{x\to 0} x (1) \\ 0 &\leq \lim\limits_{x\to 0} x \cos \left( \frac{1}{x} \right) \leq 0 \end{align*}$

Euler's Constant

Lastly, Euler’s constant $e$ can be expressed as the following limit:

$\begin{align*}e = \lim\limits_{n\to \infty} \left( 1 + \frac{1}{n} \right)^n\end{align*}$

It also holds as $n \to -\infty$:

$\begin{align*}e = \lim\limits_{n\to -\infty} \left( 1 + \frac{1}{n} \right)^n\end{align*}$

Substituting $x=\frac{1}{n}$, we can also express the limit as

$\begin{align*}e = \lim\limits_{x \to 0} \left( 1 + x \right)^\frac{1}{x}. \end{align*}$

Knowing the above limit forms of Euler’s constant allows us to compute limits that are in a similar form. For example, to compute the limit

$\begin{align*} \lim\limits_{n\to \infty} \left( 1 + \frac{2}{n} \right)^{3n} \end{align*}$

we can make a substitution that results in $\frac{2}{n} = \frac{1}{u}$. Then $n=2u$, and $n \to \infty$ translates to $u \to \infty$, and the limit becomes computable in terms of Euler’s constant:

$\begin{align*} &\lim\limits_{n\to \infty} \left( 1 + \frac{2}{n} \right)^{3n} \\ &= \lim\limits_{u\to \infty} \left( 1 + \frac{1}{u} \right)^{3 \left( 2u \right)} \\ &= \lim\limits_{u\to \infty} \left( 1 + \frac{1}{u} \right)^{6u} \\ &= \lim\limits_{u\to \infty} \left[ \left( 1 + \frac{1}{u} \right)^{u} \right]^6 \\ &= \left[ \lim\limits_{u\to \infty} \left( 1 + \frac{1}{u} \right)^{u} \right]^6 \\ &= e^6 \end{align*}$

Similarly, to compute the limit

$\begin{align*} \lim\limits_{x\to 0} \left( 1 - 3x \right)^\frac{5}{x} \end{align*}$

we can make a substitution that results in $-3x=u$. Then $x=-\frac{1}{3}u$, and $x \to 0$ translates to $u \to 0$, and the limit becomes computable in terms of Euler’s constant:

$\begin{align*} &\lim\limits_{x\to 0} \left( 1 - 3x \right)^\frac{5}{x} \\ &= \lim\limits_{u\to 0} \left( 1 +u \right)^\frac{5}{-\frac{1}{3}u} \\ &= \lim\limits_{u\to 0} \left( 1 +u \right)^{-\frac{15}{u}} \\ &= \lim\limits_{u\to 0} \left[ \left( 1 +u \right)^\frac{1}{u} \right]^{-15} \\ &= \left[ \lim\limits_{u\to 0} \left( 1 +u \right)^\frac{1}{u} \right]^{-15} \\ &= e^{-15} \end{align*}$

Exercises

Evaluate the following limits using logarithms. (You can view the solution by clicking on the problem.)

$\begin{align*}1) \hspace{.5cm} \lim\limits_{x\to 0^+} x^{(\ln x)^3} \end{align*}$

Solution:
$\infty$

$\begin{align*}2) \hspace{.5cm} \lim\limits_{x\to 0^+} x^{(\ln x)^4} \end{align*}$

Solution:
$0$

$\begin{align*}3) \hspace{.5cm} \lim\limits_{x\to 0^+} x^{\frac{1}{\ln x}} \end{align*}$

Solution:
$e$

$\begin{align*}4) \hspace{.5cm} \lim\limits_{x\to 0^+} x^{\frac{1}{(\ln x)^2}} \end{align*}$

Solution:
$1$

Evaluate the following limits using the squeeze theorem. (You can view the solution by clicking on the problem.)

$\begin{align*}5) \hspace{.5cm} \lim\limits_{x\to \infty} \frac{\sin x + \cos x}{\ln x} \end{align*}$

Solution:
$0$

$\begin{align*}6) \hspace{.5cm} \lim\limits_{x\to 0^+} \sqrt{x} \cos \left( \frac{1}{1-e^x} \right) \end{align*}$

Solution:
$0$

$\begin{align*}7) \hspace{.5cm} \lim\limits_{x\to \infty} \frac{3x+\sin x}{\sqrt{3x^2-1}} \end{align*}$

Solution:
$\sqrt{3}$

$\begin{align*}8)\hspace{.5cm} \lim\limits_{x\to 1^+} (\ln x) \sin \left( \frac{1}{\ln x} \right) \end{align*}$

Solution:
$0$

$\begin{align*}9) \hspace{.5cm} \lim\limits_{x\to -\infty} \frac{4x+3\cos x}{2x+1} \end{align*}$

Solution:
$2$

$\begin{align*}10)\hspace{.5cm} \lim\limits_{x\to \infty} \frac{2x+x\sin x}{\sqrt{x^3-4}} \end{align*}$

Solution:
$0$

Evaluate the following limits using Euler’s constant. (You can view the solution by clicking on the problem.)

$\begin{align*}11) \hspace{.5cm} \lim\limits_{n \to \infty} \left( 1 + \frac{1}{2n} \right)^{4n} \end{align*}$

Solution:
$e^2$

$\begin{align*}12) \hspace{.5cm} \lim\limits_{x \to 0} \left( 1 + \frac{2}{3}x \right)^{\frac{1}{2x}}\end{align*}$

Solution:
$e^\frac{1}{3}$

$\begin{align*}13) \hspace{.5cm} \lim\limits_{n \to -\infty} \left( 1 + \frac{5}{3n} \right)^{-2n}\end{align*}$

Solution:
$e^{ - \frac{10}{3} }$

$\begin{align*}14) \hspace{.5cm} \lim\limits_{x \to 0} \left( 1 + \frac{x}{\pi} \right)^{\frac{e}{x}}\end{align*}$

Solution:
$e^\frac{e}{\pi}$

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.