L’Hôpital’s Rule

by Justin Skycak (@justinskycak) on

When a limit takes the indeterminate form of zero divided by zero or infinity divided by infinity, we can differentiate the numerator and denominator separately without changing the actual value of the limit.

This post is part of the book Justin Math: Calculus. Suggested citation: Skycak, J. (2019). L'Hôpital's Rule. In Justin Math: Calculus. https://justinmath.com/lhopitals-rule/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

L’Hôpital’s rule provides a way to evaluate limits that take the indeterminate forms of $\frac{0}{0}$ or $\frac{\infty}{\infty}$. It says that, for such limits, we can differentiate the numerator and denominator separately, without changing the actual value of the limit.

For example, the following limit has indeterminate form.

$\begin{align*} \lim\limits_{x\to 1} \frac{\ln x}{1-x} = \frac{0}{0} \end{align*}$


Therefore, we can apply L’Hôpital’s rule to solve it.

$\begin{align*} \lim\limits_{x\to 1} \frac{\ln x}{1-x} &= \lim\limits_{x\to 1} \frac{(\ln x)'}{(1-x)'} \\ &= \lim\limits_{x\to 1} \frac{\frac{1}{x}}{-1} \\ &= \lim\limits_{x\to 1}-\frac{1}{x} \\ &= -1 \end{align*}$


Products in Indeterminate Form

Limits of the form $0 \cdot \infty$ are also indeterminate, but we need to convert them to an equivalent fraction before applying L’Hôpital’s rule.

For example, the following limit has indeterminate form of $0 \cdot \infty$, so we convert it to an equivalent fraction which has indeterminate form $\frac{\infty}{\infty}$.

$\begin{align*} \lim\limits_{x\to 0^+} \sqrt{x} \ln x &= \lim\limits_{x\to 0^+} \frac{\ln x}{\frac{1}{\sqrt{x}} } = \frac{-\infty}{\infty} \\ &= \lim\limits_{x\to 0^+} \frac{\left( \ln x \right)'}{ \left( \frac{1}{\sqrt{x} } \right)' } \\ &= \lim\limits_{x\to 0^+} \frac{\frac{1}{x}}{ -\frac{1}{2x^{3/2}} } \\ &= \lim\limits_{x\to 0^+} -2\sqrt{x} \\ &= 0 \end{align*}$


We could use other equivalent fractions, too, as long as they are equivalent to the original limit and have indeterminate form of $\frac{0}{0}$ or $\frac{\infty}{\infty}$.

However, even though L’Hôpital’s rule applies to any fraction having indeterminate form, some fractions are better than others. For example, if we wrote the previous limit as

$\begin{align*} \lim\limits_{x\to 0^+} \sqrt{x} \ln x = \lim\limits_{x\to 0^+} \frac{\sqrt{x}}{\frac{1}{\ln x}} \end{align*}$


we would still have indeterminate form and thus be able to apply L’Hôpital’s rule, but we wouldn’t get anywhere with it because the derivative of $\frac{1}{\ln x}$ gets more complex. The point of using L’Hôpital’s rule is to use differentiation to reduce the complexity of the limit, not increase it.

$\begin{align*} \lim\limits_{x\to 0^+} \sqrt{x} \ln x &= \lim\limits_{x\to 0^+} \frac{\sqrt{x} }{\frac{1}{\ln x} } = \frac{0}{0} \\ &= \lim\limits_{x\to 0^+} \frac{ \left( \sqrt{x} \right)' }{ \left( \frac{1}{\ln x} \right)' } \\ &= \lim\limits_{x\to 0^+} \frac{ \frac{1}{2 \sqrt{x} } }{ - \frac{1}{(\ln x)^2} \cdot \frac{1}{x} } \\ &= \lim\limits_{x\to 0^+} - \frac{1}{2} ( \ln x )^2 \sqrt{x} \end{align*}$


Combining L'Hôpital's Rule with Other Methods

Sometimes, we may have to use other methods in conjunction with L’Hôpital’s rule. For example, to solve the limit

$\begin{align*} \lim\limits_{x \to 0^+} \left( \frac{1}{x} \right)^x \end{align*}$


we can first compute the logarithm of the limit, using L’Hôpital’s rule.

$\begin{align*} \ln \lim\limits_{x \to 0^+} \left( \frac{1}{x} \right)^x &= \lim\limits_{x \to 0^+} \ln \left[ \left( \frac{1}{x} \right)^x \right] \\ &= \lim\limits_{x \to 0^+} x \ln \left( \frac{1}{x} \right) \\ &= \lim\limits_{x \to 0^+} -x \ln x \\ &= \lim\limits_{x \to 0^+} - \frac{\ln x}{\frac{1}{x}} = \frac{\infty}{\infty} \\ &= \lim\limits_{x \to 0^+} - \frac{(\ln x)'}{\left( \frac{1}{x} \right)' } \\ &= \lim\limits_{x \to 0^+} - \frac{\frac{1}{x} }{-\frac{1}{x^2} } \\ &= \lim\limits_{x \to 0^+} x \\ &= 0 \end{align*}$


So, we have:

$\begin{align*} \lim\limits_{x \to 0^+} \left( \frac{1}{x} \right)^x = e^0 = 1 \end{align*}$


Limits that are Not in Indeterminate Form

One BIG word of caution: L’Hôpital’s rule does NOT apply when a limit does not have indeterminate form. If you try to use L’Hôpital’s rule on a limit that does not have indeterminate form, then it may lead you to an erroneous result.

For example, the limit $\lim_{x\to \infty} \frac{\sin x}{x}$, does not take indeterminate form since the numerator does not go to zero nor infinity, and we know using the squeeze theorem that the limit evaluates to $0$. But if we apply L’Hôpital’s rule on this limit, we conclude that the limit does not exist, which is incorrect since it actually does exist and evaluates to $0$. But if we apply L’Hôpital’s rule on this limit, we conclude that the limit does not exist, which is incorrect since it actually does exist and evaluates to $0$.

$\begin{align*} \lim_{x\to \infty} \frac{\sin x}{x} &= \lim_{x\to \infty} \frac{\cos x}{1} \hspace{1.25cm} \mbox{(invalid)} \\ &= \lim_{x\to \infty} \cos x \hspace{1.35cm} \mbox{(invalid)} \\ &= \mbox{ does not exist} \hspace{.5cm} \mbox{(invalid)} \end{align*}$


Derivation and Mean Value Theorem

To see why L’Hôpital’s rule works, we can start off noticing that the limit

$\begin{align*} \lim_{x\to a} \frac{f(x)}{g(x)} = \frac{0}{0} \end{align*}$


implies that $f(a)=0$ and $g(a)=0$. This is obvious, but it’s very important to notice, because it lets us express the above limit as the ratio of difference quotients.

$\begin{align*} \lim_{x\to a} \frac{f(x)}{g(x)} &= \lim_{\Delta x\to 0} \frac{f(a+\Delta x)}{g(a+\Delta x)} \\ &= \lim_{\Delta x\to 0} \frac{f(a+\Delta x)-f(a)}{g(a+\Delta x)-g(a)} \\ &= \lim_{\Delta x\to 0} \frac{ \frac{f(a+\Delta x)-f(a)}{\Delta x} }{ \frac{g(a+\Delta x)-g(a)}{\Delta x} } \\ &= \frac{ \lim_{\Delta x\to 0} \frac{f(a+\Delta x)-f(a)}{\Delta x} }{ \lim_{\Delta x\to 0} \frac{g(a+\Delta x)-g(a)}{\Delta x} } \\ &= \frac{f'(a)}{g'(a)} \end{align*}$


This is pretty close to the full statement of L’Hôpital’s rule, but it is a bit more limited because it assumes that $g’(a)$ is nonzero – it assumes that the limit $\lim\limits_{x\to a} \frac{f’(x)}{g’(x)}$ can be evaluated through direct substitution, to yield $\frac{f’(x)}{g’(x)}$. But we have broken these assumptions in some examples, where we applied L’Hôpital’s rule multiple times in a row – in these examples, the limit still couldn’t be evaluated by direct substitution after a single iteration of L’Hôpital’s rule.

To overcome these assumptions and prove the full statement of L’Hôpital’s rule we need to understand the mean value theorem, which says that for any function $f(x)$ that is continuous on an interval $[a,b]$ and differentiable on the interval $(a,b)$, there is some point $x=c$ at which the derivative of $f$ is equal to its average rate of change:

$\begin{align*} f'(c) = \frac{f(b)-f(a)}{b-a} \end{align*}$


In other words, the mean value theorem says that if we draw a line between the endpoints of $f$, it will be parallel to the tangent line of $f$ somewhere in the interval.

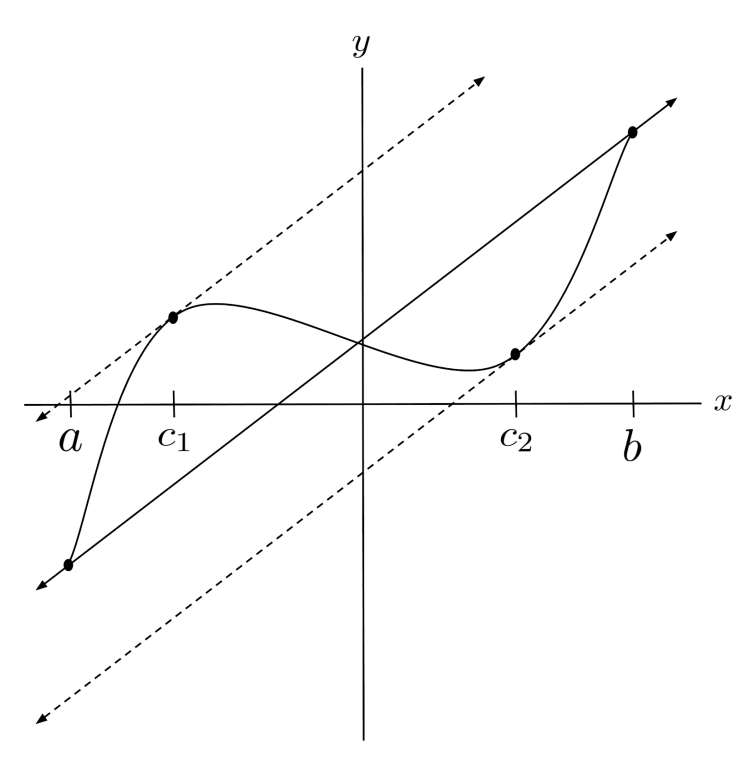
image


When fiddling with the mean value theorem, you might notice that the mean value theorem is a particular case of a more general and elegant equation, with $g(x)=x$.

$\begin{align*} \frac{f'(c)}{1} &= \frac{f(b)-f(a)}{b-a} \\ \frac{f'(c)}{g'(c)} &= \frac{f(b)-f(a)}{g(b)-g(a)} \end{align*}$


To check whether this extended result is true for any function $g(x)$, we can ask whether the derivative of the following function $h(x)$ is $0$ at some point $c \in [a,b]$.

$\begin{align*} h(x) = f(x)- \frac{f(b)-f(a)}{g(b)-g(a)} g(x) \end{align*}$


Interestingly, this function has the property $h(a)=h(b)$, so the mean value theorem tells us that, indeed, as long as $h(x)$ is continuous on an interval $[a,b]$ and differentiable on the interval $(a,b)$, then it is true that $h’(c)=0$ for some point $c \in [a,b]$. And the assumptions of continuity and differentiability are true for $h(x)$ whenever they are true for $f(x)$ and $g(x)$, so the mean value theorem does in fact extend to the result

$\begin{align*} \frac{f'(c)}{g'(c)} = \frac{f(b)-f(a)}{g(b)-g(a)}. \end{align*}$


This result is known, rather intuitively, as the extended mean value theorem.

L’Hôpital’s rule comes from applying the extended mean value theorem to the limit in question. If we have the indeterminate limit

$\begin{align*} \lim_{x\to a^+} \frac{f(x)}{g(x)} = \frac{0}{0} \end{align*}$


then we consider the interval $[a,x]$. Here, both $f(a)=0$ and $g(a)=0$, and the extended mean value theorem tells us that for some $c \in [a,x]$ we have the following:

$\begin{align*} \frac{f'(c)}{g'(c)} &= \frac{f(x)-f(a)}{g(x)-g(a)} \\ &= \frac{f(x)-0}{g(x)-0} \\ &= \frac{f(x)}{g(x)} \end{align*}$


Taking the limit as $x \to a^+$, we have $c \to a^+$ and thus

$\begin{align*} \lim\limits_{x \to a^+} \frac{f'(c)}{g'(c)} &= \lim\limits_{x \to a^+} \frac{f(x)}{g(x)} \\ \lim\limits_{x \to a^+} \frac{f'(x)}{g'(x)} &= \lim\limits_{x \to a^+} \frac{f(x)}{g(x)}. \end{align*}$


The indeterminate limit

$\begin{align*} \lim_{x\to a^-} \frac{f(x)}{g(x)} = \frac{0}{0} \end{align*}$


can be understood the same way using the interval $[x,a]$, and the indeterminate limits

$\begin{align*} \lim\limits_{x\to \infty} \frac{f(x)}{g(x)} &= \frac{0}{0} \\ \lim\limits_{x\to -\infty} \frac{f(x)}{g(x)} &= \frac{0}{0} \end{align*}$


can be understood similarly, using the intervals $[x,\infty)$ and $(-\infty,x]$. Likewise, in the case of

$\begin{align*} \lim \frac{f(x)}{g(x)} = \frac{\infty}{\infty} \end{align*}$


we can rewrite the limit as

$\begin{align*} \lim \frac{\frac{1}{f(x)}}{\frac{1}{g(x)}} = \frac{0}{0} \end{align*}$


and apply L’Hôpital’s rule, which ends up simplifying to its original form.

$\begin{align*} \lim \frac{\frac{1}{f(x)}}{\frac{1}{g(x)}} &= \lim \frac{\frac{1}{f(x)}}{\frac{1}{g(x)}} \\ \lim \frac{\frac{1}{f(x)}}{\frac{1}{g(x)}} &= \lim \frac{\left( \frac{1}{f(x)} \right)'}{\left( \frac{1}{g(x)}\right)'} \\ \lim \frac{\frac{1}{f(x)}}{\frac{1}{g(x)}} &= \lim \frac{-\frac{f'(x)}{f(x)^2}}{-\frac{g'(x)}{g(x)^2}} \\ \lim \frac{\frac{1}{f(x)}}{\frac{1}{g(x)}} &= \lim \frac{f'(x)}{g'(x)} \cdot \frac{g(x)^2}{f(x)^2} \\ \lim \frac{g(x)}{f(x)} &= \lim \frac{f'(x)}{g'(x)} \cdot \frac{g(x)^2}{f(x)^2} \\ \lim \frac{g(x)}{f(x)} \cdot \frac{f(x)^2}{g(x)^2} &= \lim \frac{f'(x)}{g'(x)} \\ \lim \frac{f(x)}{g(x)} &= \lim \frac{f'(x)}{g'(x)} \end{align*}$


Exercises

Evaluate the indicated limits by applying L’Hôpital’s rule. (You can view the solution by clicking on the problem.)

$\begin{align*}1) &\hspace{.5cm} \lim\limits_{x \to 0} \frac{\sin x}{x} \end{align*}$
Solution:
$\begin{align*} 1 \end{align*}$


$\begin{align*}2) &\hspace{.5cm} \lim\limits_{x \to 0} \frac{1-\cos x}{x} \end{align*}$
Solution:
$\begin{align*} 0 \end{align*}$


$\begin{align*}3) &\hspace{.5cm} \lim\limits_{x \to \frac{\pi}{2} } \frac{\tan x}{\frac{\pi}{2}-x} \end{align*}$
Solution:
$\begin{align*} \infty \end{align*}$


$\begin{align*}4) &\hspace{.5cm} \lim\limits_{x \to 0^+} \frac{(\ln x)^2}{x} \end{align*}$
Solution:
$\begin{align*} \infty \end{align*}$


$\begin{align*}5) &\hspace{.5cm} \lim\limits_{x \to 1} \frac{x \ln x}{x^2-1} \end{align*}$
Solution:
$\begin{align*} \frac{1}{2} \end{align*}$


$\begin{align*}6) &\hspace{.5cm} \lim\limits_{x \to 0^+} (\ln x) \tan x \end{align*}$
Solution:
$\begin{align*} 0 \end{align*}$


$\begin{align*}7) &\hspace{.5cm} \lim\limits_{x \to \frac{\pi}{2} } (\tan x)^{\cos x} \end{align*}$
Solution:
$\begin{align*} 1 \end{align*}$


$\begin{align*}8) &\hspace{.5cm} \lim\limits_{x \to \infty} x^{ \frac{1}{\sqrt{x}} } \end{align*}$
Solution:
$\begin{align*} 1 \end{align*}$


$\begin{align*}9) &\hspace{.5cm} \lim\limits_{x \to 0} (\cos x)^{\frac{1}{x^2}} \end{align*}$
Solution:
$\begin{align*} \frac{1}{\sqrt{e}} \end{align*}$


$\begin{align*}10) &\hspace{.5cm} \lim\limits_{x \to \infty} x^{ \frac{1}{\ln x} } \end{align*}$
Solution:
$\begin{align*} e \end{align*}$


This post is part of the book Justin Math: Calculus. Suggested citation: Skycak, J. (2019). L'Hôpital's Rule. In Justin Math: Calculus. https://justinmath.com/lhopitals-rule/


Want to get notified about new posts? Join the mailing list and follow on X/Twitter.