Horizontal Asymptotes of Rational Functions

by Justin Skycak (@justinskycak) on May 02, 2018

Rational functions can have a form of end behavior in which they become flat, approaching (but never quite reaching) a horizontal line known as a horizontal asymptote.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Horizontal Asymptotes of Rational Functions. In Justin Math: Algebra. https://justinmath.com/horizontal-asymptotes-of-rational-functions/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Like polynomials, rational functions can have end behavior that goes to positive or negative infinity. However, rational functions can also have another form of end behavior in which they become flat, approaching (but never quite reaching) a horizontal line known as a horizontal asymptote.

Demonstration

For example, consider the rational function $r(x)=\frac{3x-2}{4x+1}$. As we input larger and larger numbers in the positive direction, the function output becomes closer and closer to $0.75$.

$\begin{align*} r(10) &= \frac{28}{41} \approx 0.683 \\ r(100) &= \frac{298}{401} \approx 0.743 \\ r(1000) &= \frac{2998}{4001} \approx 0.749 \end{align*}$

The same thing happens as we input larger and larger numbers in the negative direction: the function output becomes closer and closer to $0.75$.

$\begin{align*} r(-10) &= \frac{-32}{-39} \approx 0.821 \\ r(-100) &= \frac{-302}{-399} \approx 0.757 \\ r(-1000) &= \frac{-3002}{-3999} \approx 0.751 \end{align*}$

As a result, we say that the function $r$ has a horizontal asymptote at $y=0.75$.

Why Horizontal Asymptotes Occur

To understand why this happens, take a look at the function in proper form, $r(x) = \frac{3}{4} + \frac{11/4}{4x+1}$.

When we input a very large positive or negative number, remainder fraction’s denominator becomes much larger than its numerator, causing the remainder fraction to shrink to $0$.

On the other hand, the $\frac{3}{4}$ term persists, which causes the output to be close to $\frac{3}{4}$ or $0.75$.

$\begin{align*} r(\text{large number}) &= \frac{3}{4} + \frac{11/4}{\text{large number}} \\ &\approx \frac{3}{4} + 0 \\ &= 0.75 \end{align*}$

Perhaps even more intuitively, notice that when we input very large values of $x$ into $\frac{3x-2}{4x+1}$, the leading (highest degree) terms in the numerator and denominator become so much larger than the other terms, that the other terms cease to matter. The fraction then becomes approximately the ratio of the leading terms, $\frac{3x}{4x}$, which simplifies to $\frac{3}{4}$, or $0.75$ in decimal form.

Case when the Denominator has Greater Degree

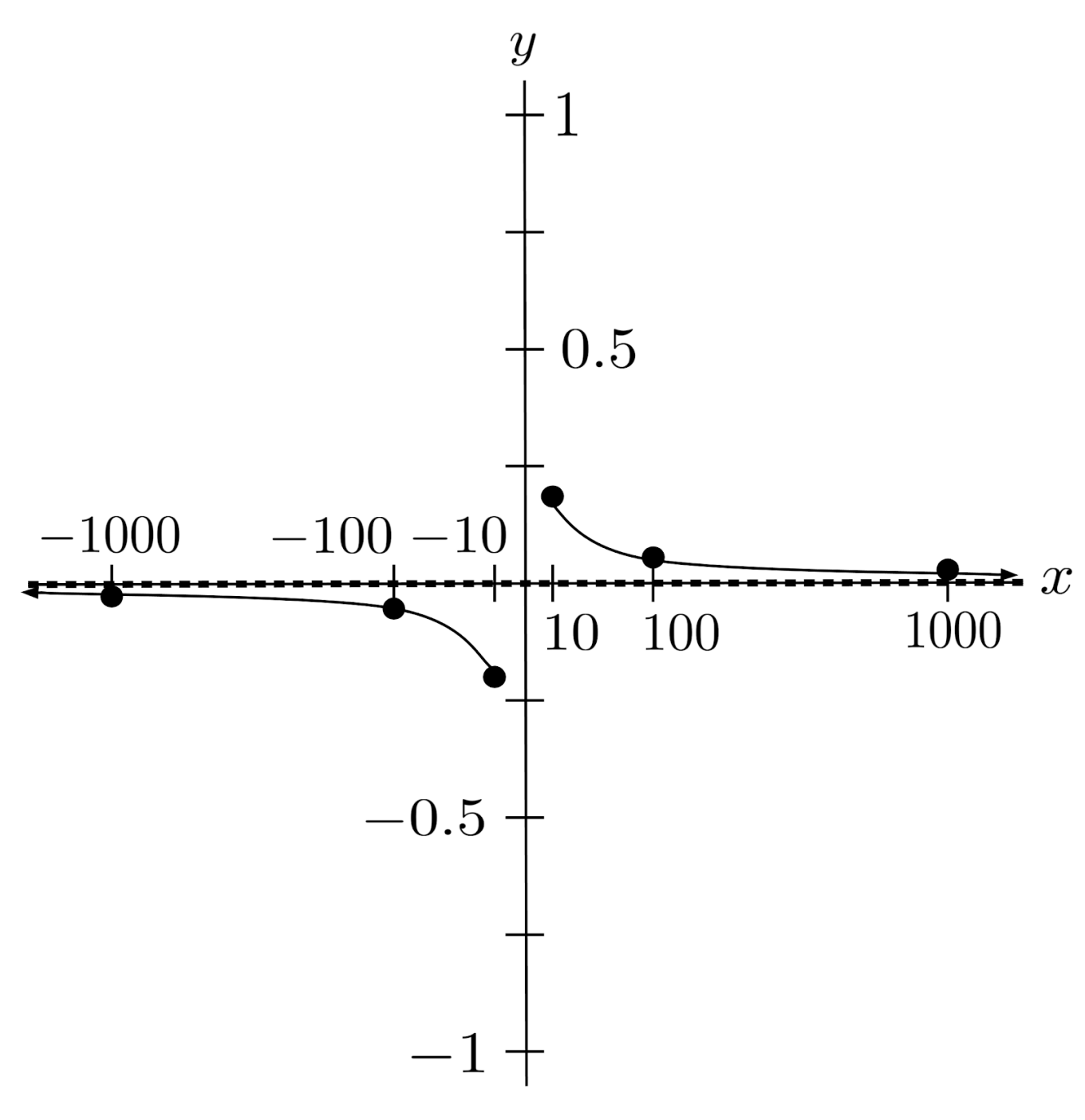
Now consider the case when the denominator is of a greater degree than the numerator – say, when $r(x)=\frac{2x+1}{x^2-1}$.

Again, when we input very large values of $x$ into the function, the leading terms in the numerator and denominator become the only terms that matter. The fraction then becomes approximately $\frac{2x}{x^2}$, which simplifies to $\frac{2}{x}$.

When we input very large values for $x$, the denominator becomes very large while the numerator stays the same, causing the fraction to shrink to $0$. As a result, the function has a horizontal asymptote at $0$.

We can confirm this by evaluating the function.

$\begin{align*} &r(10) = \frac{21}{99} \approx 0.212 \hspace{.5cm} && r(-10) = \frac{-19}{99} \approx -0.192 \\ &r(100) = \frac{201}{9999} \approx 0.020 && r(-100) = \frac{-199}{9999} \approx -0.019 \\ &r(1000) = \frac{2001}{999999} \approx 0.002 && r(-1000) = \frac{-1999}{999999} \approx -0.002 \\ \end{align*}$

Case when the Numerator has Greater Degree

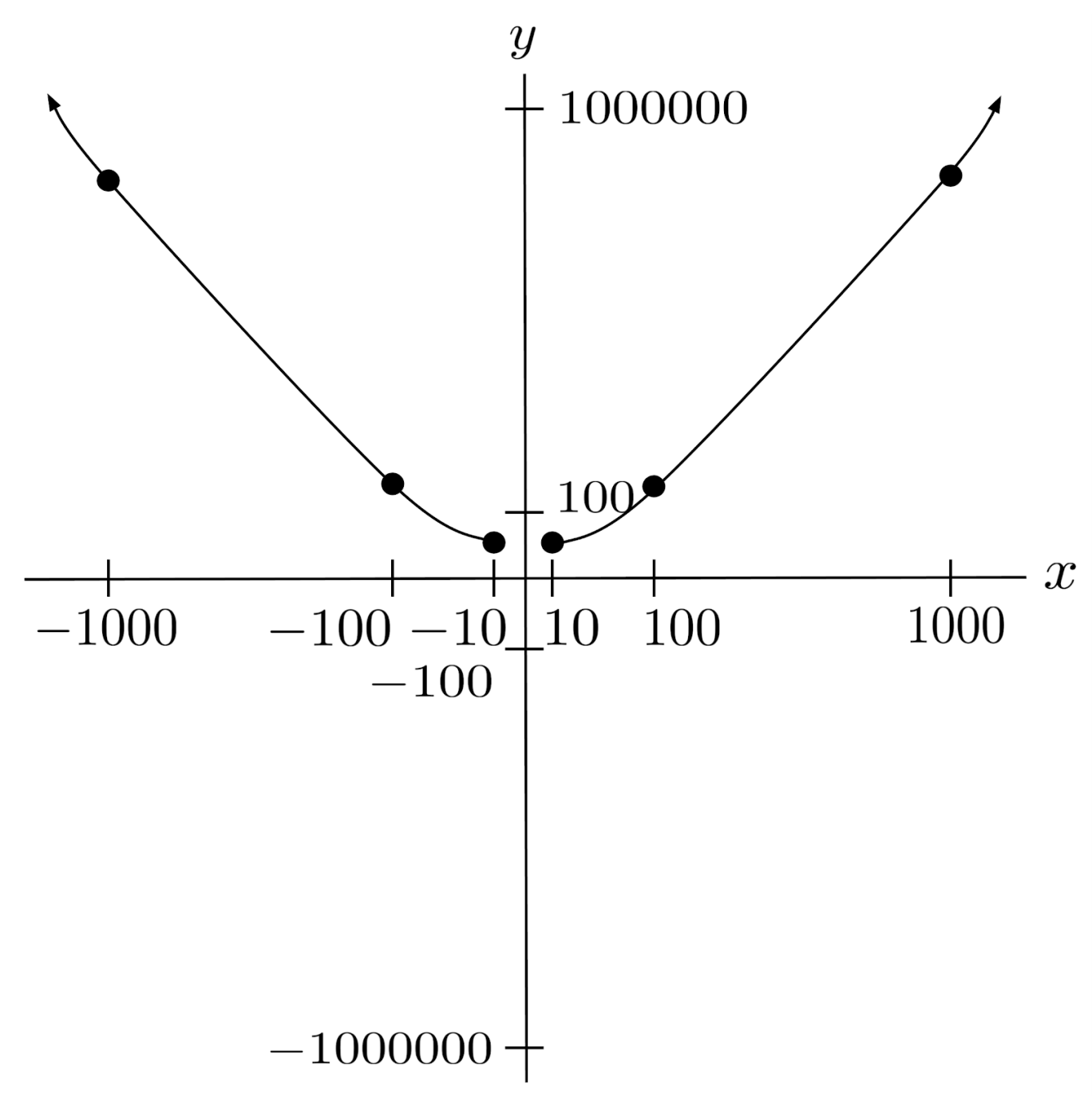
Lastly, consider a rational function whose numerator is of greater degree than its denominator – say, $r(x)=\frac{3x^3+2x+1}{5x-2}$.

Taking the ratio of leading terms, we have $\frac{3x^3}{5x}$, which simplifies to $\frac{3}{5}x^2$. This expression grows without bound when we input large values of $x$, so the function has no horizontal asymptote.

We can confirm this by evaluating the function.

$\begin{align*} &r(10) \approx 63 \hspace{.5cm} && r(-10) \approx 58 \\ &r(100) \approx 6025 \hspace{.5cm} && r(-100) \approx 5976 \\ &r(1000) \approx 600240 \hspace{.5cm} && r(-1000) \approx 599760 \end{align*}$

Exercises

Find the horizontal asymptote, if any, of each rational function. (You can view the solution by clicking on the problem.)

$1) \hspace{.5cm} r(x)=\dfrac{5x^3+3x-2}{x^3+2x^2-x}$

Solution:
$y=5$

$2) \hspace{.5cm} r(x)=\dfrac{6x^7+7x^6+x^2+1}{-3x^7+4x^5-x^3+2}$

Solution:
$y=-2$

$3) \hspace{.5cm} r(x)=\dfrac{x^5+5x-4}{2x^3+1}$

Solution:
$\text{none}$

$4) \hspace{.5cm} r(x)=\dfrac{-8x^7+4x^4-7x^2}{-7x^{10}+2x+1}$

Solution:
$y=0$

$5) \hspace{.5cm} r(x)=\dfrac{(x^2+4)(3x^5+7x^2+2)}{(3x^4+5)(2x^3-x^2-3)}$

Solution:
$y=\frac{1}{2}$

$6) \hspace{.5cm} r(x)=\dfrac{(2-3x^2)(x^3-2x^2+5)}{(2x+3)(x^2+1)(x^2-1)}$

Solution:
$y=-\frac{3}{2}$

$7) \hspace{.5cm} r(x)=\dfrac{(x+1)(x-2)(x+3)}{(x^2+7)(8+x^3)}$

Solution:
$y=0$

$8) \hspace{.5cm} r(x)=\dfrac{(x+1)^3(2x^2+3x+4)}{(4x^2+7x-8)^2}$

Solution:
$\text{none}$

$9) \hspace{.5cm} r(x)=\dfrac{(x+5)^2(2x+3)^3}{(3x^2-2)(3x^3+5)}$

Solution:
$y=\frac{8}{9}$

$10) \hspace{.5cm} r(x)=\dfrac{x(1-2x)^3(x+2)}{(4x-1)(2-x)^4}$

Solution:
$y=-2$

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.