Elimination as Vector Reduction

by Justin Skycak (@justinskycak) on

If we interpret linear systems as sets of vectors, then elimination corresponds to vector reduction.

This post is part of the book Justin Math: Linear Algebra. Suggested citation: Skycak, J. (2019). Elimination as Vector Reduction. In Justin Math: Linear Algebra. https://justinmath.com/elimination-as-vector-reduction/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Recall that systems of linear equations can be solved through elimination, multiplying equations by constants and adding equations to each other to cancel variables.

For example, to solve the following linear system

$\begin{align*} x+2y+3z &= 2 \\ -x-y-2z &= 1 \\ 2x+4y+7z &= 5 \end{align*}$


we can start by adding the first equation to the second equation and subtracting two times the first equation from the third equation.

$\begin{align*} &x+2y+3z = 2 \\ &(-x-y-2z = 1) + (x+2y+3z = 2) \\ &(2x+4y+7z = 5) - 2(x+2y+3z = 2) \\ &\text{ } \\ &x+2y+3z = 2 \\ &(-x-y-2z) + (x+2y+3z) = 1+2 \\ &(2x+4y+7z) - 2(x+2y+3z) = 5 - 2(2) \\ &\text{ } \\ &x+2y+3z = 2 \\ &y+z = 3 \\ &z =1 \end{align*}$


Then, starting with $z=1$, we can back-substitute to solve for each of the variables:

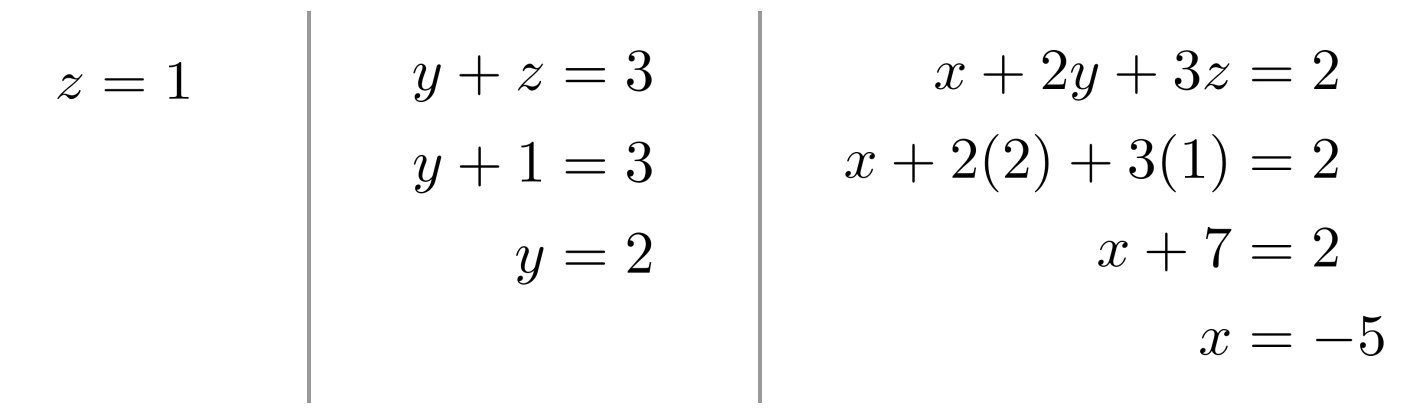
image


We reach the final solution $x=-5$, $y=2$, and $z=1$.

Interpreting Elimination as Vector Reduction

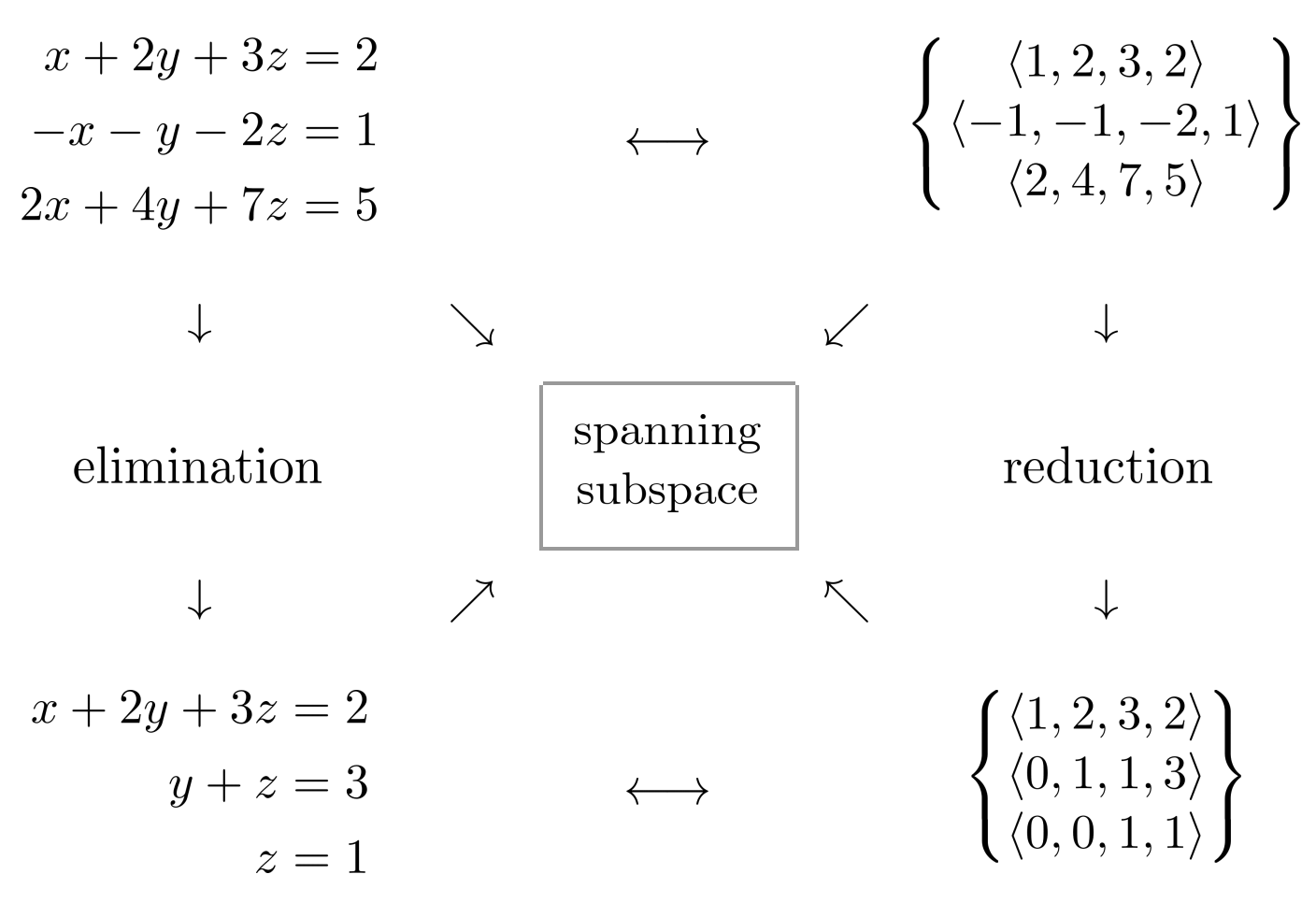
In light of the previous chapter, elimination can also be interpreted as vector reduction.

First, we can interpret the linear system itself as a set of vectors, consisting of the coefficients and constants.

$\begin{align*} \left\lbrace \begin{matrix} x&+2y&+3z &= 2 \\ -x&-y&-2z &= 1 \\ 2x&+4y&+7z &= 5 \end{matrix} \right\rbrace \longrightarrow \left\lbrace \begin{matrix} \left< 1,2,3,2 \right> \\ \left< -1,-1,-2,1 \right> \\ \left< 2,4,7,5 \right> \end{matrix} \right\rbrace \end{align*}$


Then, to reduce the set of vectors, we can add the first equation to the second equation, and subtract two of the first equation from the third equation.

$\begin{align*} \left\lbrace \begin{matrix} \left< 1,2,3,2 \right> \\ \left< -1,-1,-2,1 \right> + \left< 1,2,3,2 \right> \\ \left< 2,4,7,5 \right> - 2\left< 1,2,3,2 \right> \end{matrix} \right\rbrace \end{align*}$


$\begin{align*} \left\lbrace \begin{matrix} \left< 1,2,3,2 \right> \\ \left< 0,1,1,3 \right> \\ \left<0,0,1,1 \right> \end{matrix} \right\rbrace \end{align*}$


Then, we can convert the set of vectors back into equations that can be solved in the same way via back-substitution.

$\begin{align*} \left\lbrace \begin{matrix} \left< 1,2,3,2 \right> \\ \left< 0,1,1,3 \right> \\ \left<0,0,1,1 \right> \end{matrix} \right\rbrace \longrightarrow \left\lbrace \begin{matrix} x&+2y&+3z &= 2 \\ &y&+z &= 3 \\ & & z &=1 \end{matrix} \right\rbrace \end{align*}$


The big geometric insight here is that the space of linear equations is actually a vector space.

This occurs because we’re allowed to add/subtract multiples of the equations. The particular linear equations in our system span a subspace of this vector space, and reducing the vectors allows us to simplify the system while maintaining the original span.

image


Thinking of linear equations in terms of vectors can sometimes yield additional insight. For example, notice that for a system of linear equations to have a single solution, the vectors must be reducible to the following form:

$\begin{align*} \left\lbrace \begin{matrix} \left< 1, \square, \square, \cdots, \square, \square \right> \\ \left< 0,1, \square, \cdots, \square, \square \right> \\ \vdots \\ \left<0,0, 0, \cdots, 1, \square \right> \end{matrix} \right\rbrace \end{align*}$


In other words, the vectors must span all components except the last. For a system of linear equations in $n$ variables, the vectors consist of $n+1$ components: the first $n$ components correspond to variable coefficients, and the last component corresponds to the constant.

As a result, for a system of linear equations in $n$ variables to have a single solution, at least $n$ equations are required.

Exercises

Solve the following systems. (You can view the solution by clicking on the problem.)

$\begin{align*} 1) \hspace{.5cm} 2x+3y &= 1 \\ x+y &= 1 \end{align*}$
Solution:
$\begin{align*} x &= 2 \\ y &= -1 \end{align*}$


$\begin{align*} 2) \hspace{.5cm} x-2y &= -1 \\ 2x-y &= 7 \end{align*}$
Solution:
$\begin{align*} x &= 5 \\ y &= 3 \end{align*}$


$\begin{align*} 3) \hspace{.5cm} x+2y-z &= 2 \\ 2x+y+z &= 7 \\ x+y-2z &= -3 \end{align*}$
Solution:
$\begin{align*} x &= 1 \\ y &= 2 \\ z &= 3 \end{align*}$


$\begin{align*} 4) \hspace{.5cm} 3x-4y+z &= 8 \\ 3x+y &= 5 \\ y+z &= -3 \end{align*}$
Solution:
$\begin{align*} x &= 2 \\ y &= -1 \\ z &= -2 \end{align*}$


$\begin{align*} 5) \hspace{.5cm} x+2z &= 3 \\ x+y &= 6 \\ y-z &= 4 \end{align*}$
Solution:
$\begin{align*} x &= 1 \\ y &= 5 \\ z &= 1 \end{align*}$


$\begin{align*} 6) \hspace{.5cm} -x+5y &= -7 \\ 3x+3z &= 15 \\ x+y+z &= 4 \end{align*}$
Solution:
$\begin{align*} x &= 2 \\ y &= -1 \\ z &= 3 \end{align*}$


$\begin{align*} 7) \hspace{.5cm} w+x-y-z &= 4 \\ 2w-x &= 1 \\ x+y+z &= 4 \\ x+2z &= 5 \end{align*}$
Solution:
$\begin{align*} w &= 2 \\ x &= 3 \\ y &= 0 \\ z &= 1 \end{align*}$


$\begin{align*} 8) \hspace{.5cm} 3w+2x+y &= -5 \\ 3x+2y+z &= -2 \\ w+2y+3z &= 1 \\ w-x-y-z &= -1 \end{align*}$
Solution:
$\begin{align*} w &= -1 \\ x &= 0 \\ y &= -2 \\ z &= 2 \end{align*}$


This post is part of the book Justin Math: Linear Algebra. Suggested citation: Skycak, J. (2019). Elimination as Vector Reduction. In Justin Math: Linear Algebra. https://justinmath.com/elimination-as-vector-reduction/


Want to get notified about new posts? Join the mailing list and follow on X/Twitter.