Derivatives and the Difference Quotient

by Justin Skycak on

The derivative of a function is the function's slope at a particular point, and can be computed as the limit of the difference quotient.

This post is a chapter in the book Justin Math: Calculus. Suggested citation: Skycak, J. (2019). Derivatives and the Difference Quotient. Justin Math: Calculus. https://justinmath.com/derivatives-and-the-difference-quotient/

The derivative of a function is the function’s slope at a particular point. We can approximate the derivative at a point $(x,f(x))$ by choosing another nearby point on the function, and computing the slope. If we increase the input $x$ by a small amount $\Delta x$, then we reach an x-coordinate of $x+\Delta x$, and the corresponding point on the function is $(x+\Delta x, f(x+\Delta x))$.

icon


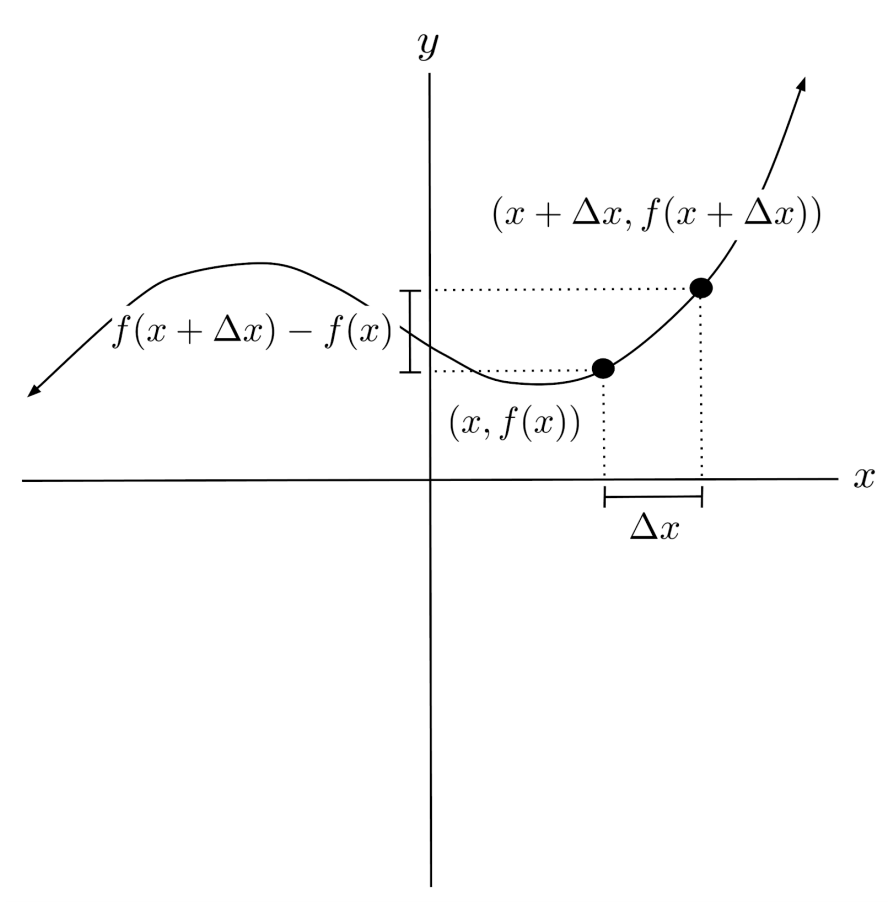
We compute the slope between the points $(x,f(x))$ and $(x+\Delta x, f(x+\Delta x))$, and simplify.

$\begin{align*} m &= \frac{f(x+\Delta x) - f(x)}{x+\Delta x - x} \\ &= \frac{f(x+\Delta x) - f(x)}{\Delta x } \end{align*}$


The above expression is called the difference quotient of the function $f$. As the point $(x+\Delta x, f(x+\Delta x))$ gets closer and closer to the point $(x, f(x))$, the difference quotient becomes a better and better approximation for the exact slope at $(x,f(x))$.

icon


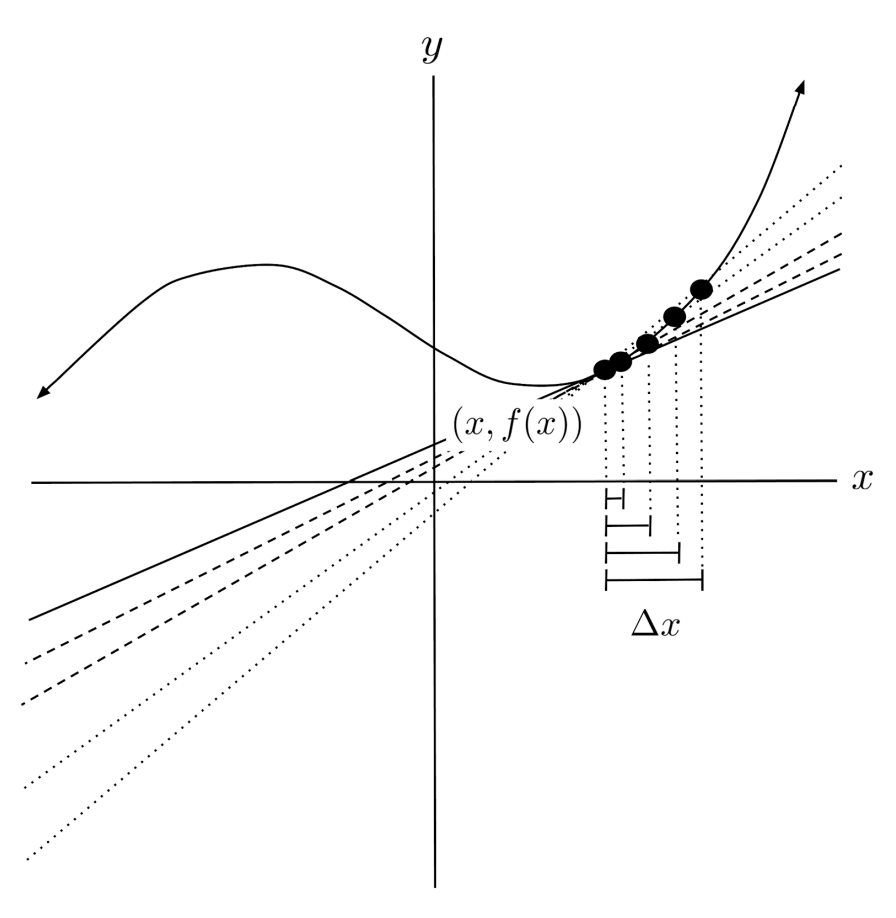
Thus, we can compute derivative, which is the exact slope at $(x,f(x))$, by taking the limit as the second point approaches the first point. In other words, the derivative is the limit of the difference quotient as the difference $\Delta x$ between the two input x-values approaches $0$.

$\begin{align*} \frac{d}{dx} f(x) = \lim_{\Delta x \to 0} \frac{f(x+\Delta x) - f(x)}{\Delta x} \end{align*}$


The derivative of the function $f$ at the point $(x,f(x))$ is indicated by the notation $\frac{d}{dx} f(x)$. However, to simplify notation, we often write the derivative as $f’(x)$ instead of $\frac{d}{dx} f(x)$.

Demonstration

As an example, we’ll use the difference quotient show that the derivative of $f(x)=x^2$ is $f’(x)=2x$.

$\begin{align*} f'(x) &= \lim_{\Delta x \to 0} \frac{(x+\Delta x)^2 - x^2}{\Delta x} \\ &= \lim_{\Delta x \to 0} \frac{x^2+(2\Delta x)x + (\Delta x)^2 - x^2}{\Delta x} \\ &= \lim_{\Delta x \to 0} \frac{(2\Delta x)x + (\Delta x)^2}{\Delta x} \\ &= \lim_{\Delta x \to 0} 2x + \Delta x \\ &= 2x + 0 \\ &= 2x \end{align*}$


This means that the slope of $f(x)=x^2$ at any point $(x,f(x))$ is given by $f’(x)=2x$.

In particular, the slope at $x=-3$ is given by $f’(-3)=-6$, the slope at $x=0$ is given by $f’(0)=0$, and the slope at $x=3$ is given by $f’(3)=6$.

Looking at the graph, these values make sense:

  • • At $x=-3$, the graph is falling down at a steep angle, which matches the negative derivative $f'(-3)=-6$.
  • • At $x=0$, the graph is flat at the bottom of a valley, which matches the negative derivative $f'(0)=0$.
  • • At $x=3$, the graph is climbing up at a steep angle, which matches the negative derivative $f'(3)=6$.
icon


The values for the derivative also make sense numerically:

  • • If we start at the point $(-3,9)$ and pick another point $(-2.999,8994001)$ on the function $f(x)=x^2$, the slope between the two points is $\frac{8.994001-9}{-2.999-(-3)}=-5.999$, which approximates our derivative value $f'(-3)=-6$.
  • • If we start at the point $(0,0)$ and pick another point $(0,001,0,000001)$ on the function $f(x)=x^2$, the slope between the two points is $\frac{0.000001-0}{0.001-0}=0.001$, which approximates our derivative value $f'(0)=0$.
  • • If we start at the point $(3,9)$ and pick another point $(3.001,9.006001)$ on the function $f(x)=x^2$, the slope between the two points is $\frac{9.006001-9}{3.001-3}=6.001$, which approximates our derivative value $f'(3)=6$.

Exercises

Use the difference quotient to differentiate the following functions. (You can view the solution by clicking on the problem.)

$\begin{align*}1) \hspace{.5cm} f(x)=5x \end{align*}$
Solution:
$\begin{align*} f'(x)=5 \end{align*}$

$\begin{align*}2) \hspace{.5cm} f(x)=-3x+1 \end{align*}$
Solution:
$\begin{align*} f'(x)=-3 \end{align*}$

$\begin{align*}3) \hspace{.5cm} f(x)=x^2 \end{align*}$
Solution:
$\begin{align*} f'(x)=2x \end{align*}$

$\begin{align*}4) \hspace{.5cm} f(x)=7x^2 \end{align*}$
Solution:
$\begin{align*} f'(x)=14x \end{align*}$

$\begin{align*}5) \hspace{.5cm} f(x)=x^2-x \end{align*}$
Solution:
$\begin{align*} f'(x)=2x-1 \end{align*}$

$\begin{align*}6) \hspace{.5cm} f(x)=x^3 \end{align*}$
Solution:
$\begin{align*} f'(x)=3x^2 \end{align*}$

$\begin{align*}7) \hspace{.5cm} f(x)=2\sqrt{x} \end{align*}$
Solution:
$\begin{align*} f'(x)=\frac{1}{\sqrt{x}} \end{align*}$

$\begin{align*}8)\hspace{.5cm} f(x) = \sqrt{3x} \end{align*}$
Solution:
$\begin{align*} f'(x)= \frac{ \sqrt{3} }{2 \sqrt{x} } \end{align*}$

$\begin{align*}9) \hspace{.5cm} f(x) = \frac{1}{x} \end{align*}$
Solution:
$\begin{align*} f'(x)= -\frac{1}{x^2} \end{align*}$

$\begin{align*}10) \hspace{.5cm} f(x) = \frac{1}{2x+1} \end{align*}$
Solution:
$\begin{align*} f'(x)= -\frac{2}{(2x+1)^2} \end{align*}$


This post is a chapter in the book Justin Math: Calculus. Suggested citation: Skycak, J. (2019). Derivatives and the Difference Quotient. Justin Math: Calculus. https://justinmath.com/derivatives-and-the-difference-quotient/